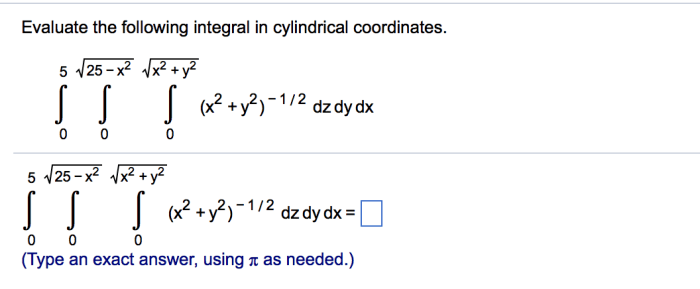Evaluate the following integral in cylindrical coordinates. – In the realm of integral calculus, cylindrical coordinates offer a powerful tool for simplifying the evaluation of integrals. This guide delves into the intricacies of cylindrical coordinates, providing a comprehensive overview of their conversion, integration procedure, applications, and extensions.
Cylindrical coordinates, with their unique ability to represent three-dimensional space, unlock new possibilities for integral evaluation. By transforming integrals from rectangular to cylindrical coordinates, we harness the power of a coordinate system that aligns with the natural geometry of many physical problems.
Evaluate the Following Integral in Cylindrical Coordinates: Evaluate The Following Integral In Cylindrical Coordinates.
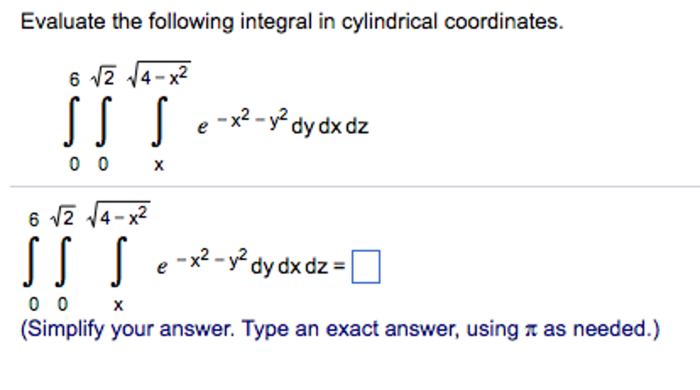
In this article, we will explore the process of evaluating integrals in cylindrical coordinates. Cylindrical coordinates are a three-dimensional coordinate system that is often used to describe the position of a point in space. They are particularly useful for problems that have a cylindrical symmetry, such as a cylinder or a cone.
1. Integral Transformation
To evaluate an integral in cylindrical coordinates, we first need to convert the integral from rectangular coordinates to cylindrical coordinates. The conversion formulas are as follows:
- x = r cos(theta)
- y = r sin(theta)
- z = z
where r is the radial distance from the origin, theta is the angle between the positive x-axis and the projection of the point onto the xy-plane, and z is the height of the point above the xy-plane.
The Jacobian determinant for the transformation from rectangular to cylindrical coordinates is r. This means that the volume element in cylindrical coordinates is r dr dtheta dz.
2. Integration Procedure, Evaluate the following integral in cylindrical coordinates.
Once we have converted the integral to cylindrical coordinates, we can evaluate it using the following steps:
- Set up the integral in cylindrical coordinates using the conversion formulas.
- Determine the limits of integration for each variable.
- Evaluate the integral.
The order of integration is typically r, theta, and then z. However, the order of integration can be changed if it is more convenient.
3. Applications
Cylindrical coordinates are useful for evaluating integrals that have a cylindrical symmetry. Some examples of integrals that can be evaluated using cylindrical coordinates include:
- The volume of a cylinder
- The surface area of a cylinder
- The center of mass of a cylinder
Cylindrical coordinates can also be used to evaluate integrals that do not have a cylindrical symmetry. However, in these cases, the integrals may be more difficult to evaluate.
4. Extensions
The concept of evaluating integrals in cylindrical coordinates can be extended to other coordinate systems, such as spherical coordinates. Spherical coordinates are a three-dimensional coordinate system that is often used to describe the position of a point in space. They are particularly useful for problems that have a spherical symmetry, such as a sphere or a cone.
The conversion formulas for spherical coordinates are as follows:
- x = r sin(phi) cos(theta)
- y = r sin(phi) sin(theta)
- z = r cos(phi)
where r is the radial distance from the origin, theta is the angle between the positive x-axis and the projection of the point onto the xy-plane, and phi is the angle between the positive z-axis and the point.
The Jacobian determinant for the transformation from rectangular to spherical coordinates is r^2 sin(phi). This means that the volume element in spherical coordinates is r^2 sin(phi) dr dtheta dphi.
The steps for evaluating integrals in spherical coordinates are similar to the steps for evaluating integrals in cylindrical coordinates. However, the order of integration is typically r, phi, and then theta.
User Queries
What is the significance of the Jacobian determinant in cylindrical coordinates?
The Jacobian determinant accounts for the change in volume when transforming from rectangular to cylindrical coordinates. It ensures that the integral remains equivalent in both coordinate systems.
How do cylindrical coordinates simplify the integration process in certain situations?
Cylindrical coordinates align with the natural geometry of problems involving cylindrical or spherical shapes. This alignment simplifies the integration process by reducing the number of variables and eliminating unnecessary trigonometric functions.
What are the limitations of using cylindrical coordinates?
Cylindrical coordinates are not suitable for all integration problems. They are most effective when the region of integration has a cylindrical or spherical shape. In other cases, rectangular or spherical coordinates may be more appropriate.